Altitudes and the Orthic Triangle of Triangle ABC

Given a triangle ABC with acute angles, let A*, B*, C* be the feet of the altitudes of the triangle: A*, B*, C* are points on the sides of the triangle so that AA* BB*, CC* are altitudes.

Then we have proved earlier that the altitudes are concurrent at a point H. (The proof used the relationship between the perpendicular bisectors of the sides of a triangle and the altitudes of its midpoint triangle).

The orthic triangle of ABC is defined to be A*B*C*. This triangle has some remarkable properties that we shall prove:

1. The altitudes and sides of ABC are interior and exterior angle bisectors of orthic triangle A*B*C*, so H is the incenter of A*B*C* and A, B, C are the 3 ecenters (centers of escribed circles).
2. The sides of the orthic triangle form an "optical" or "billiard" path reflecting off the sides of ABC.
3. From this it can be proved that the orthic triangle A*B*C* has the smallest perimeter of any triangle with vertices on the sides of ABC.

Part 1: Prove that the altitudes and sides of ABC are angle bisectors of A*B*C*

Lemma 1. Continuing with the same figure, the circle c₃ with diameter AB intersects AC at B* and BC as A*.

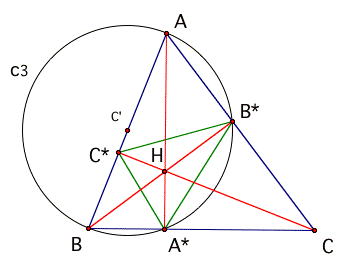
Proof. The center of the circle is the midpoint C' of AB. By the inscribed angle theorem (Carpenter theorem), since AC'B is a diameter and a straight angle, for any point P on c₃, the angle APB is a right angle. Thus the circle intersects AC at a point P so that BP is perpendicular to AC; the only such point is P = B*. Likewise, the circle intersects BC at A*.

Lemma 2. Continuing with the same figure, angle ABB* = angle AA*B*.

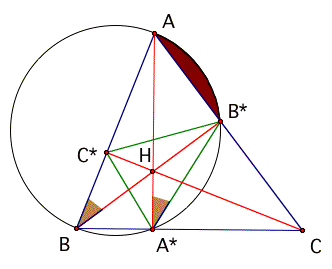
Proof: Both angles are angles inscribed in circle c with diameter AB. They both equal half the arc angle of arc B*A. Thus they are equal.

Corollary. Continuing with the same figure, angle ACC* = angle AA*C*.

Proof: Just replace B with C in the Lemma 2.

Lemma 3. Continuing with the same figure, angle AA*C*= angle AA*B*. In other words A*A bisects angle A* of triangle A*B*C*.

Proof. We have seen already from Lemma 2 that angle AA*B*. = angle ABB* and angle AA*C*. = angle ACC*.

But angle ABB* = angle ACC* by similar triangles. Both triangles ABB* and ACC* are right triangles with right angles at B* and C* and a shared angle at A, so by AA, triangles ABB* is similar to triangle ACC* and thus the angles are equal.

Corollary: In the figure above, angle C*A*B = angle B*A*C and line BC bisects the exterior angles at A* of triangle A*B*C*.

Proof: The exterior angle bisector at A* is the line through A* perpendicular to the interior angle bisector, which was proved to be A*A. Thus BC is this line.

If we set x = angle AA*C*= angle AA*B*, then angle C*A*B = 90 – x = angle B*A*C. Each angle is also half of an exterior angle obtained by extending a side of A*B*C*.

Theorem: If A*B*C* is the orthic triangle of ABC, then the altitudes of ABC bisect the interior angles of A*B*C* and the sides of ABC bisect the exterior angles.

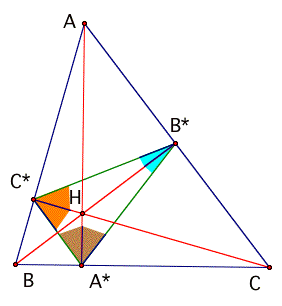
Proof. This was proved for vertex A* in Lemma 3 and its Corollary. Since A* could be chosen to be any vertex of A*B*C*, this proves the theorem for the vertices at B* and C* by the same reasoning.

Corollary: The orthocenter H of ABC is the incenter of A*B*C*, and A, B and C are the ecenters of A*B*C*. Thus four circles tangent to lines A*B*, B*C*, C*A* can be constructed with centers A, B, C, H.

Relation between the Orthocenter and the Circumcircle

The triangle ABC can be inscribed in a circle called the circumcircle of ABC. There are some remarkable relationships between the orthocenter H and the circumcircle.

The altitude line CC* intersects the circumcircle in two points. One is C. Denote the other one by C**.

Proposition. The point CC* is the reflection of H in line AB.

This implies that the figure HBC**A is a kite, and C* is the midpoint of H and C**.

Proof: We have seen in Lemma 3 above that the triangles ABB* and ACC* are similar, so that angle ABB* is congruent to angle ACC*.

But angle ACC* is the same angle as angle ACC** is the same angle as angle C*BC**.

Angle ABB* is the same angle as angle ABH is the same as angle C*BH.

Angle ACC** is an inscribed angle subtending the same arc as angle ABC**, so these two angles are equal. Thus all 3 angles are congruent: angle C*BH = angle ACC* = angle C*BC**.

Applying this proposition to each altitude, we get this theorem.

Theorem. Given an acute triangle ABC inscribed in a circle c. Let A**, B***, C*** be the intersections of the altitudes of ABC with the circle (besides A, B, C, which are also intersections). Then these points are reflections of H in the sides of ABC and triangle A**B**C** is similar to the orthic triangle A*B*C*. In fact the dilation with center H and ratio 1/2 takes A**B**C** to A*B*C*.